math.luga.ru : Матбой Лужские группы ЗМШ

Math.luga.ru : г. Луга Ленинградской области. Математический сайт

Главная • Информация • ФотоАльбом • Гостевая • Форум • Письмо

Математический бой между сборными командами Лужских групп ЗМШ и Академической гимназии СПбГУ (СПб, АГ СПбГУ, 2 декабря 2009 г.)

Задачи

1. На огороженном поле 1 км × 1 км построили заборы, разделившие его на прямоугольные участки 5 м × 20 м и 6 м × 12 м. Какой может быть общая длина построенных заборов?

2. В треугольнике

выполняется равенство $\tg A \cos B=\sin C$ . Докажите, что в этом треугольнике биссектриса одного из углов, медиана, проведённая из вершины другого, и высота, опущенная из третьего угла, пересекаются в одной точке.

3. Сумма трёх положительных чисел

равна 1. Какое наименьшее значение может принимать сумма $\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}$ ?

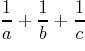4. Доступ к сейфу имеют 7 человек. Каким наименьшим количеством замков следует снабдить сейф, чтобы никакие трое, собравшись вместе, не смогли его открыть, а любые четверо — смогли? (Укажите, как надо распределить ключи от замков между этими 7 людьми.)

5. Можно ли многочлен

представить в виде разности квадратов двух многочленов различных степеней?

6. В окружность вписан четырёхугольник ABCD. Пусть E — точка пересечения прямых AB и CD, F — прямых AD и BC. Биссектриса угла AEC пересекает сторону BC в точке M и сторону AD в точке N, а биссектриса угла BFD пересекает сторону AB в точке P и сторону CD в точке Q. Докажите, что четырёхугольник MPNQ — ромб.

7. В шахматном турнире участвуют 30 человек (каждый играет по одной партии с каждым; за победу даётся 1 очко, за ничью — 0,5 очка, за поражение — 0 очков). Чтобы выполнить норму разрядника, надо набрать не менее 60% возможных очков. Какое наибольшее число шахматистов смогут стать разрядниками по итогам этого турнира?

8. Последовательность задана формулой общего члена:

. Какое наибольшее количество членов, кратных 5, может оказаться среди 2009 последовательных членов данной последовательности?

9. Какой минимальный диаметр должен иметь круг, которым можно покрыть любой многоугольник с периметром P ?

10. Имеются шесть коробочек: красная, оранжевая, жёлтая, зелёная, голубая и синяя, а также 6 шариков — по одному каждого из указанных цветов. Сколькими способами шарики можно разложить по одному в коробочки так, чтобы ни для одной коробки её цвет не совпал с цветом шарика?

Команды

Команда 1:
Курицын Михаил (ЗМШ, капитан), Сафаров Дмитрий (АГ, зам. капитана), Арефьев Сергей (ЗМШ), Белехов Иван (ЗМШ), Думченко Святослав (АГ), Илюхина Александра (АГ), Кащеев Антон (АГ), Лосьянов Игорь (АГ).

Команда 2:
Шалагинов Вячеслав (ЗМШ, капитан), Михеев Владислав (Сиверская гимназия, зам. капитана), Архангельский Роман (ЗМШ), Кокарев Александр (АГ), Ларкин Сергей (ЗМШ), Миронова Светлана (АГ), Мусин Роман (АГ), Протасова Надежда (АГ).

Примечания:
АГ — Академическая гимназия СПбГУ,
ЗМШ — Лужские группы Заочной математической школы.

Итог боя:

Главная • Информация • ФотоАльбом • Гостевая • Форум • Письмо