1.1. Может ли число, у которого все цифры — семёрки, делиться на число, у которого все цифры — девятки?
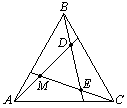
1.2.
Лучи
,
и 
попарно пересекаются внутри равностороннего треугольника
, причём
(см. рисунок).
Верно ли, что треугольник 
—
тоже равносторонний?
1.3. Сколько корней имеет уравнение
2.1. На острове Ламашан живёт несколько шуршавчиков, у которых в среднем по 1876 шуршалок. Когда один из шуршавчиков раздарил все свои шуршалки другим шуршавчикам этого острова и покинул его, среднее число шуршалок у каждого из оставшихся шуршавчиков стало равно 2010. Сколько шуршавчиков осталось на острове Ламашан?
2.2. Произведение двух натуральных чисел, каждое из которых не делится на 10, равно 1000. Докажите, что их сумма делится на 7.
2.3. Сто сумасшедших последовательно красят доску 100×100, используя сто цветов и соблюдая правило: ни в одном столбце и ни в одной строке не может оказаться двух клеток, раскрашенных в один цвет. Обязательно ли 99 сумасшедших смогут докрасить доску, если первый уже раскрасил 100 клеток?
3.1.
Найдите все 
, 
,
, удовлетворяющие системе
3.2.
На гипотенузе 
прямоугольного треугольника
выбрана точка 
так,
что 
.
Отрезок 
пересекает биссектрису 
в её середине.
Найдите острые углы треугольника .
3.3.
Саша утверждает, что число
можно представить в виде суммы двух квадратов натуральных чисел.
А Серёжа говорит, что это можно сделать не менее чем двумя способами.
Кто прав?
4.1. В 8А классе мальчиков больше, чем девочек. Во вторник каждый мальчик купил пирожок, а каждая девочка — булочку, а в среду наоборот: каждый мальчик купил по булочке, а девочка — по пирожку. Оказалась, что во вторник ученики 8А класса вместе потратили на 1 рубль меньше, чем в среду. Что дороже, пирожок или булочка, и на сколько, если их цены отличаются более чем на 50 копеек?
4.2. Противоположные стороны AB и CD выпуклого четырёхугольника ABCD лежат на перпендикулярных прямых. Расстояние между серединами сторон BC и AD равно 7. Найдите расстояние между серединами диагоналей AC и BD.
4.3. Можно ли на клетчатом поле 6×6 расставить 5 шахматных коней так, чтобы они били все свободные клетки доски?
| фамилии, имена участников команд (класс) | номер команды, школа |
сумма баллов | диплом |
|---|---|---|---|
| Григорий Коренёк (7 кл.), Александр Лучко (8 кл.), Артём Николаев (7 кл.), Евгения Самодумова (7 кл.), Герман Севостьянов (7 кл.), Денис Семёнов (8 кл.) | № 5, Лужская СОШ № 3 | 25 | I |
| Анастасия Алексеева (7 кл.), Алексей Ананьев (8 кл.), Александр Березовский (8 кл.), Георгий Лязев (8 кл.), Дарья Пивоварова (7 кл.), Никита Постнов (7 кл.) | № 1, Сиверская гимназия | 15 | II |
| Алексей Афанасьев (7 кл.), Елена Безымянных (7 кл.), Илья Захаров (8 кл.), Давид Косян (8 кл.), Павел Сухов (7 кл.), Наталья Фёдорова (8 кл.) | № 4, Гатчинская СОШ № 8 | 13 | III |
| Сергей Архипов (8 кл.), Дарья Вологдина (7 кл.), Екатерина Данильченко (8 кл.), Виктор Зуев (7 кл.), Анастасия Хмелевская (7 кл.), Ксения Цветкова (7 кл.) | № 2, Сиверская гимназия | 8 | |
| София Измайлова (8 кл.), Евгений Колесов (7 кл.), Анна Кузенкова (7 кл.), Алексей Смольянинов (7 кл.), Анжелика Трофимова (8 кл.), Ирина Шигицева (8 кл.) | № 3, Гатчинская СОШ № 8 | 7 | |
| Анастасия Гитлина (8 кл.), Егор Голованов (8 кл.), Лев Кеворков (7 кл.), Сергей Лучко (8 кл.), Тимур Мамаджанов (8 кл.), Мария Чуприна (7 кл.) | № 6, Лужская СОШ № 3 | 4 |
