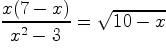Math.luga.ru  :  г. Луга Ленинградской области. Математический сайт
Главная • Информация • ФотоАльбом • Гостевая • Форум • Письмо
Система Orphus
Олимпиада математико-механического факультета СПбГУ. 2008 год
Олимпиада проходила на математико-механическом факультете СПбГУ 9 марта 2008 г.

Условия задач. Вариант 1

1.  Какое максимальное значение может иметь сумма первых восьми членов арифметической прогрессии, у которой сумма квадратов первого, четвёртого и седьмого членов равна 2  ?

2.  Решить уравнение $\dfrac{x(7-x)}{x^2-3}=\sqrt{10-x}$.

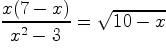3.  Решить неравенство $\log_{6-4x} |x| \cdot \log_3\left|\dfrac{18}{x}-12\right| \geqslant 1$.

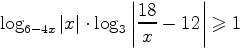4.  В трапецию с основаниями 4 и 12 помещены две окружности, касающиеся друг друга внешним образом. Каждая из окружностей касается боковых сторон и одного из оснований. Найти радиус окружности, касающейся большего основания, если известно, что расстояние между точками касания, лежащими на боковой стороне трапеции, равно 6.

5.  Решить уравнение $\arcsin\left(\dfrac{4}{3}-x\right) - \arcsin (x-1) = \dfrac{2\pi}{3}$.

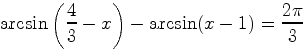6.  Имеется два бака с водой $A$  и $B$. Одновременно из каждого бака отбирают треть содержимого. Отобранное из $A$ выливают в $B$, а отобранное из $B$ — в $A$. После того, как операцию повторили ещё два раза, в баке $A$ оказался 351 литр воды. Затем операцию повторили ещё три раза. Сколько воды стало в $A$, если в $B$в этот момент оказалось $b$ литров? Указать, при каких значениях $b$ задача имеет решение.

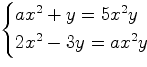7.  При каких значениях параметра $a$  система  $\begin{cases} ax^2+y=5x^2y\\ 2x^2-3y=ax^2y \end{cases}$ имеет единственное решение?

Условия задач. Вариант 2

1.  Какое минимальное значение может иметь сумма первых девяти членов арифметической прогрессии, у которой сумма квадратов третьего, четвёртого и пятого членов равна 2 ?

2.  Решить уравнение .

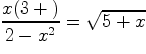3.  Решить неравенство $\log_{7-5x} |x| \cdot \log_2\left|\dfrac{14}{x}-10\right| \leqslant 1$.

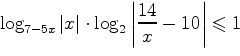4.  В трапецию с основаниями 4 и 8 помещены две окружности, касающиеся друг друга внешним образом. Каждая из окружностей касается боковых сторон и одного из оснований. Найти радиус окружности, касающейся меньшего основания, если известно, что расстояние между точками касания, лежащими на боковой стороне трапеции, равно 4.

5.  Решить уравнение $\arccos\left(\dfrac{3}{2}-x\right) + \arccos\left(\dfrac{1}{2}-x\right) = \dfrac{2\pi}{3}$.

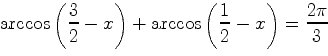6.  Имеется два бака с водой $A$  и $B$. Одновременно из каждого бака отбирают четверть содержимого. Отобранное из $A$ выливают в $B$, а отобранное из $B$ — в $A$. После того, как операцию повторили ещё три раза, в баке $A$ оказалось 340 литров воды. Затем операцию повторили ещё два раза. Сколько воды стало в $B$, если в $A$  в этот момент оказалось $a$ литров? Указать, при каких значениях $a$ задача имеет решение.

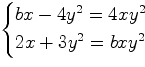7.  При каких значениях параметра $b$  система  $\begin{cases} bx-4y^2=4xy^2\\ 2x+3y^2=bxy^2 \end{cases}$ имеет единственное решение?



  Последнее обновление 17 марта 2008 года
Главная • Информация • ФотоАльбом • Гостевая • Форум • Письмо
© math.luga.ru, 2002–2017. Все права защищены. При цитировании ссылка обязательна