Math.luga.ru  :  г. Луга Ленинградской области. Математический сайт
Главная • Информация • ФотоАльбом • Гостевая • Форум • Письмо
Система Orphus
Задачи второго (муниципального) этапа XXXIV Всероссийской олимпиады школьников по математике (Ленинградская область) (2007–2008 уч. год)

9 класс

1.  Что больше: $65^{7}$ или $127^{6}$ ?

2.  Найдите наименьшее целое положительное $n$ такое, что если к десятичной записи $n$ приписать слева 2, а справа 1, то новое число будет равно $33n$.

3.  Каждый лотерейный билет имеет трёхзначный номер, составленный из цифр 1, 2, 3. Каждый билет открашен в один из цветов: красный, синий, зелёный. Если два билета имеют номера, которые отличаются во всех трёх разрядах, то билеты имеют разные цвета. Билет 122 — красный, билет 222 — зелёный. Какого цвета билет 123 ?

4.  В треугольнике $ABC$  точка $D$ — середина $AB$, точка $E$ лежит на $BC$ , так что $BE=2EC$  и $\angle ADC=\angle BAE$ . Найдите $\angle BAC$ .

5.  Число 27000001 имеет ровно четыре простых делителя. Найдите их сумму.

10 класс

1.  Можно ли расположить на плоскости 2007 прямых так, чтобы они пересекались ровно в 14006 точках и никакие три из них не пересекались бы в одной точке?

2.  Пётр и Павел играют в следующую игру. Пётр называет два ненулевых целых числа $m$  и $n$. Павел записывает квадратную функцию с коэффициентами 2007, $m$,  $n$  (в любом порядке). Пётр выигрывает в том и только том случае, если соответствующее квадратное уравнение имеет два различных рациональных корня, иначе выигрывает Павел. Докажите, что Пётр всегда может выиграть.

3.  Из двух арифметических прогрессий $\left\{a_{i}\right\}$  и $\left\{b_{i}\right\}$ составлена новая последовательность $a_{1}b_{1}$, $a_{2}b_{2}$, ... . Первые три члена новой последовательности равны соответственно 1440, 1716, 1848. Найдите восьмой член новой последовательности.

4.  В треугольнике на рисунке числа означают площади соответствующих треугольников. Найдите $x$ — площадь четырёхугольника.

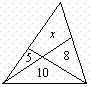
5.  Решите уравнение  $4x^2-40[x]+51=0$ .

11 класс

1.  Найдите пять семизначных чисел, делящихся на 35, десятичная запись которых содержит только цифры 5 и 7.

2.  Пётр и Павел играют в игру: они по очереди ставят коэффициенты в уравнение  $x^{3}+...x^{2}+...x+...=0$ : Пётр — на любое из трёх свободных мест, затем Павел — на любое из двух оставшихся, потом Павел — на последнее из оставшихся. Докажите, что при любой игре Павла Пётр может добиться того, что уравнение будет иметь три корня.

3.  Целые числа  $a$,  $b$,  $c$,  $d$  таковы, что $0<a<b<c<d$, числа $a$,  $b$,  $c$,  образуют арифметическую прогрессию, числа  $b$,  $c$,  $d$, — геометрическую и $d-a=30$.  Найдите $a+b+c+d$.

4.  Пусть $a,b>0$,  $a\ne b$. Два равнобедренных треугольника со сторонами $x$, $x$,  $a$  и   $x$, $x$,  $b$  имеют равные площади. Найдите $x$ .

5.  Найдите количество корней уравнения
$$x=\left[\dfrac{x}{2}\right] + \left[\dfrac{x}{3}\right] + \left[\dfrac{x}{5}\right].$$



  Последнее обновление 3 декабря 2007 года
Главная • Информация • ФотоАльбом • Гостевая • Форум • Письмо
© math.luga.ru, 2002–2017. Все права защищены. При цитировании ссылка обязательна