Всероссийский конкурс решения задач

[PSP]

ЕЩЁ ОДНУ ПОПЫТКУ

предприняла Фёдорова Алина, пытаясь решить задачу № 3.

Эх, если бы и другие преодолели лень и проявили активность...

[PSP]

РЕШЕНИЕ ЗАДАЧИ № 3

на учебных сборах 24 сентября расскажет Тюков Даниил.

[PSP]

РЕШЕНИЕ ЗАДАЧИ №4 ПОЧТИ ГОТОВО

Есть надежда, что Павлова Людмила внесёт очередную правку, и на учебных сборах 24 сентября мы сможем это решение обсудить.

[PSP]

РЕШЕНИЯ ЗАДАЧ № 1 и № 4

на учебных сборах 24 сентября расскажет Павлова Людмила.

Как бы проснуться и всем остальным!

[PSP]

На учебных сборах 24 сентября были рассказаны решения задач № 1, № 4 (Павлова Людмила) и № 3 (Тюков Даниил).
МОЛОДЦЫ!

[PSP]

Задачи 2-го тура
(срок отправки решений - до 1 ноября 2019 г)

5. По кругу выписаны 10 целых чисел. Петя нашел десять сумм двух рядом стоящих чисел.
а) Могли ли все эти суммы оказаться последовательными числами?
б) Могли ли 9 из них оказаться последовательными числами?

6. Барон Мюнхгаузен заявил, что какой бы ему ни дали треугольник, он сможет разрезать его на два многоугольника, а потом каждый из них разрезать на 7 равных многоугольников. Могут ли слова барона быть правдой?

7. Возьмём любое натуральное число, например, 2019. Составим второе число, которое показывает, сколько и каких цифр (в порядке возрастания) содержит исходное число. Получится 10111219, что означает «один нуль, одна единица, одна двойка и одна девятка». На основе второго числа по тому же принципу образуем третье число 10511219, потом – четвёртое 1041121519, и т. д.
а) Квантик убеждён, что с какого бы числа ни начать, в получившейся последовательности какое-то число непременно встретится дважды. Ноутик считает, что не обязательно – возможна последователь¬ность, в которой все числа различны. Кто прав?
б) Могут ли в такой последовательности встретиться два одинаковых числа подряд?

8. Докажите для всех натуральных n:

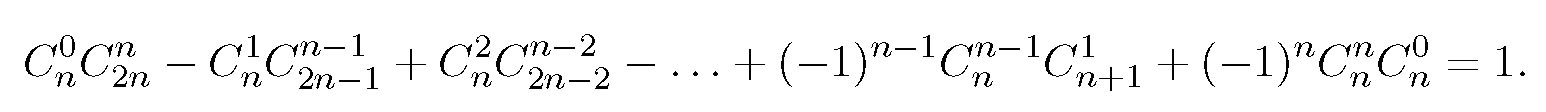
Задача 8.jpg (27.82 КБ) 18123 просмотра

(Через

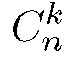
Задача 8_2.jpg (11.47 КБ) 18123 просмотра

обозначается количество способов выбрать k предметов из n различных предметов.)

[PSP]

И снова первым проснулся Даня

Тюков Даниил уже решил одну из задач и прислал оформленное её решение.
Подъём, все остальные!

[PSP]

И ЕЩЁ ПОЛЗАДАЧИ!

Сделана задача № 7б. Нетрудно угадать, кем... Её решил Тюков Даня.

[PSP]

НАЧАЛ РЕШАТЬ ЗАДАЧИ ЕЩЁ ОДИН ЧЕЛОВЕК!

Это Титеева Нелли. Она прислала решение задачи № 5б.

А остальные 93 человека сладко (горько?) спят...

[PSP]

ХОРОШЕЕ ДВИЖЕНИЕ ВПЕРЁД

произошло, благодаря Тюкову Даниилу, решившему ещё одну задачу.

[PSP]

ЕЩЁ ОДНА РАДОСТЬ

Титеева Нелли прислала решение задачи № 7б.

[PSP]

РЕЗУЛЬТАТ ПРОВЕРКИ РАБОТЫ 1-го ТУРА

Московское жюри проверило нашу работу:
1) +
2) +
3) +
4) +

МОЛОДЦЫ!

О результатах наших соперников несколько позже.

[PSP]

МЫ И НАШИ СОПЕРНИКИ (1-й тур)

Среди групп мы - лучшие.

Что касается индивидуальных участников, то столько же задач (все четыре), как и мы, решили:

- семиклассник из Москвы (наш давний конкурент),

- восьмиклассница из Болгарии (тоже давно нам известная),

- шестиклассник из Москвы (новый конкурент).

[PSP]

Задачи 3-го тура
(срок отправки решений - до 1 декабря 2019 г)

9. Петя и Вася тренируются на кольцевом велотреке: одновременно стартовали из одной и той же точки и едут с постоянными скоростями. Петя едет быстрее Васи. Когда Петя прошёл 16 кругов, он встретил в точке старта Васю. А когда Вася прошёл 16 кругов, он встретилв точке старта Петю. Верно ли, что Вася после каждого круга встречал в точке старта Петю?

10. У Саши есть два клетчатых квадрата 7×7. Ему нужно разрезать их по линиям сетки на части так, чтобы частей получилось не более пяти и их можно было уложить в один слой в коробку 10 × 10. Есть ли способ выполнить это задание?

11. Даны отрезок AB и окружность. Постройте на окружности точки C и D так, чтобы четырёхугольник ABCD был равнобокой трапецией с основанием AD.

12. По кругу выписано 2019 натуральных чисел. За одну операцию можно либо удвоить одно из этих чисел, либо прибавить к нему одного из его соседей. Всегда ли можно за несколько операций сделать все числа равными?

[PSP]

И СНОВА ОН - ПЕРВЫЙ!

Тюков Даниил первым прислал решение задачи 3-го тура.
Он справился с заданием № 10.

Павлова Людмила также прислала верное решение этой задачи (несколько позже Дани).

Прислала решение задачи № 10 и Фёдорова Алина,но она при чтении условия пропустила некоторые слова, без которых задача превратилась в упражнение для 1-го класса.

Фёдорова Алина также попыталась решить задачу № 11, но тут ей, видимо, показалось, что в условии задачи есть некоторые слова, которых на самом деле в условии нет...

А ВСЕ ОСТАЛЬНЫЕ СПЯТ?

Спокойной ночи_70.jpg (60.03 КБ) 17510 просмотров