Всероссийский конкурс решения задач

[PSP]

В НАШЕМ "ПОЛКУ" ЕЩЁ ПРИБЫЛО!
И нас стало шестеро...

Попросили прислать решение задачи № 16, предложенное Сергеевым Артёмом,
Еронин Валерий, Фёдорова Алина, Титеева Нелли. Им выслана копия письма Сергеева Артёма.
Есть вопросы - пишите Артёму!

19 декабря после матбоя состоялся разговор с Артёмом. Павлова Людмила сказала, что она, как ей кажется, поняла идею решения и готова оформить решение. Сам Артём тоже обещал прислать откорректированное решение в удобочитаемом виде.

Советую каждому, кто сумеет вникнуть в мысли Артёма, оформить решение этой задачи и прислать его по эл. почте.
Затем мы вместе выберем то, которое и отправим в Москву. Время ещё есть.

[PSP]

ХОРОШО, ХОРОШО!

Сергеев Артём прислал откорректированное решение задачи № 16.

Это решение отправлено всем пятерым НЕСПЯЩИМ (см. выше).
Если кто-то ещё заинтересовался - пишите!

[PSP]

ЕЩЁ ЛУЧШЕ!

Своё решение задачи № 16 прислал Еронин Валерий.
Это решение отправлено всем НЕСПЯЩИМ (см. выше).

Задачу обсудим на учебных сборах 24 декабря.

[PSP]

ПРЕДНОВОГОДНЯЯ НОВОСТЬ

После обсуждения на учебных сборах 24 декабря различных решений задачи № 16 (спасибо Сергееву Артёму, Еронину Валерию) Павлова Людмила оформила решение для отправки в Москву.

Решения задач 4-го тура будут отправлены в жюри конкурса 30 декабря.
Любой желающий может получить решение любой из задач и проверить его.

[PSP]

Задачи 5-го тура
(срок отправки решений - до 1 февраля 2020 г)

17. Барон Мюнхгаузен огородил свои владения забором в форме n-угольника. Он утверждает, что каждый внутренний угол этого n-угольника либо меньше 10 градусов, либо больше 350 градусов. Может ли барон быть прав?
Решите задачу для а) n = 10; б) n = 11; в) n = 101.
Интересно также подумать над общим случаем: что получается при всех n?

18. Вычислите сумму

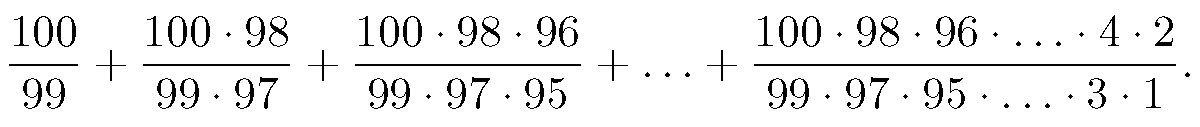
Задача 18.jpg (34.51 КБ) 16976 просмотров

19. Квантик и Ноутик по очереди закрашивают клетки на доске 8×8, по одной клетке за ход, начинает Квантик. Первый ход можно сделать куда угодно. Каждый следующий ход должен быть таким, что новая клетка граничит по стороне ровно с одной закрашенной клеткой. Кто не может сделать ход, проиграл. Кто может обеспечить себе победу?

20. В каждой вершине правильного 4k-угольника сидело по блохе. Каждая блоха дружит с двумя своими соседями. Половина блох — красные, половина — синие, причем красные и синие блохи чередуются. Блохи начали прыгать. В первую секунду прыгнули красные: каждая прыгнула в точку, симметричную ей относительно прямой, соединяющей двух её друзей. Во вторую секунду аналогичным образом прыгнули все синие блохи. В третью секунду снова прыгнули все красные и т. д. Докажите, что через k секунд все блохи снова окажутся в вершинах некоторого правильного 4k-угольника.

[PSP]

ПЕРВОЕ ПРОДВИЖЕНИЕ В 5-м ТУРЕ

совершил Еронин Валерий. Он прислал решение задачи № 19.
Своё решение он расскажет на учебных сборах 14 января.

[PSP]

РАБОТАЮТ ПОКА ТОЛЬКО ТРОЕ

Павлова Людмила прислала решение задачи № 18.

Тюков Даниил прислал (из Сочи) решения задач № 17 и № 18.

Решения задач № 17, № 18, № 19 рассмотрим на учебных сборах 14 января.

Совсем глухо с задачей № 20.

Трудная-задача_70.jpg (78.46 КБ) 16908 просмотров

[PSP]

В 5-м ТУРЕ ОСТАЛОСЬ РЕШИТЬ ЗАДАЧУ № 20

14 января на учебных сборах рассмотрены решения задач №№ 17, 19.

В присланном Тюковым Даниилом решении задачи № 17 найдены несколько "дыр". Благодаря слаженной работе Павловой Людмилы, Пластун Виктории, Щербины Якова, Еронина Валерия, Крутелёва Кирилла, эти дыры в основном залатаны. Оформлением решения занимается Павлова Людмила.

Присланное Ерониным Валерием решение задачи № 19 признано верным.

Решение задачи № 18 будет рассмотрено на учебных сборах 21 января.

[PSP]

РЕЗУЛЬТАТ ПРОВЕРКИ РАБОТЫ 4-го ТУРА

Московское жюри проверило нашу работу:
13 ) +
14 ) +
15 ) +
16 ) +

МОЛОДЦЫ!

[PSP]

ЧИТАЙТЕ, ПРОВЕРЯЙТЕ!

Оформленное Людмилой Павловой решение задачи № 17 отправлено участникам учебных сборов.

[PSP]

МЫ И НАШИ СОПЕРНИКИ (4-й тур)

Среди групп мы - одна из двух лучших команд (наравне с нами - команда московских 8-9-классников).

Что касается индивидуальных участников, то по 4 задачи решили 7-классник из Москвы, 8-классница из Болгарии и 9-классник из Москвы.

[PSP]

Задачи 6-го тура
(срок отправки решений - до 1 марта 2020 г)

21. Число 1210 автобиографичное: его первая цифра показывает, сколько в нём нулей, вторая — сколько единиц, третья — сколько двоек, а четвёртая — сколько троек. Найдите следующее автобиографичное целое число.

22. В прямоугольный треугольник вписаны два квадрата, как показано на рисунке. Докажите, что три отмеченные точки лежат на одной прямой.

22.jpg (48.59 КБ) 16661 просмотр

23 Числа x, y, z положительные и xyz = 1. Докажите неравенство

23.jpg (23.17 КБ) 16661 просмотр

24. В левой нижней клетке квадратного поля 10 × 10 стоит красная фишка, в правой верхней — синяя. За один шаг красная фишка перемещается на соседнее поле либо вверх, либо вправо; а синяя — либо вниз, либо налево. Фишка не может вставать на поле, на котором сейчас стоит другая фишка. Фишки делают шаги по очереди: начинает красная, потом ходит синяя, потом снова красная и т. д., пока каждая фишка не займёт угол, противоположный своему начальному углу. Сколько есть способов совершить такие передвижения?

[PSP]

ЛУЖАНЕ ОБЪЯВИЛИ ОТВЕТ НА ЗАДАЧУ № 21

На занятии 5 февраля Даувальтер Роберт назвал автобиографическое число, которое больше указанного в условии, и объявил его следующим. Но чёткого доказательства, увы, привести не смог.

Крылов Тимофей пообещал прислать такое доказательство.

[PSP]

ЗАДАЧА № 21 РЕШЕНА И В ГАТЧИНЕ, И В ЛУГЕ

решения задачи прислали Павлова Людмила и Крылов Тимофей.

Их решения мы рассмотрим, соответственно, на учебных сборах 11 февраля и на занятии 12 февраля.

[PSP]

ЕСТЬ РЕШЕНИЕ ЗАДАЧИ № 22

Его прислал Павлова Людмила.
Решение будет рассмотрено на учебных сборах 11 февраля.